WCT Noise Modeling
(top) (pkg)

A WCT spectral object must provide these attributes:

nsamples

an integer number providing the size of (number of contiguous time series samples taken from) the waveforms used to form the mean spectral amplitude. The nsamples must not count any zero padding that may have been applied to a waveform prior to forming the waveform contribution to the mean spectrum (ie, prior to applying the DFT). The nsamples value is distinct from the size of the freqs and amps arrays. If using NoiseTools::Collector the value for nsamples is provided by the .nticks() method.

period

a floating-point number providing the original sample period (inverse of sampling frequency) of the waveform expressed in the WCT system of units for [time]. (eg, 0.5*us for MicroBooNE). Note, period is not necessarily related to the values provided by the freqs array.

freqs

an array of floating-point numbers providing frequency values expressed in the WCT system of units for [frequency]. Note, WCT’s base unit for [frequency] is not 1.0 Hz. The size of this array must be equal to the size of the amps array and an element of freqs must provide the frequency at which the corresponding element of the amps array was sampled. The freqs array may represent an irregular sampling and may be unordered. It should include samples at or near the zero and Nyquist frequencies. In particular it need not be a regular frequency sampling of 1/period nor extend beyond the Nyquist frequency.

amps

an array of floating-point numbers providing an estimate of a mean spectral amplitude in units of [voltage] in the WCT system of units. Note that here “amps” an abbreviation of “amplitude” and not “amperage”. The value of an element of amps may be derived from some sub-sampling or interpolation of an original distribution of DFT coefficients. That is, an element of amps is the an average \(\langle|X_k|\rangle,\ k\in [0,N^{(fft)}-1]\) with \(N^{(fft)} \ge\) nsamples, over some number of waveforms of size nsamples. The inequality is typically due to zero-padding of the waveform prior to taking the DFT. Note: in preparing amps the user is recommended to provide a number of waveforms approximately equal to nsamples in order to co-optimize spectral resolution and statistical stability. User is also recommended to utilize NoiseTools::Collector for low-level noise modeling code or execute a job using NoiseModeler for a high-level development.

The EmpiricalNoiseModel component requires these optional attributes:

const

a floating point number expressed in the same units as amps and which provides an estimate of the mean white noise, and thus constant, spectral amplitude \(\langle|X_w|\rangle\).

gain

a floating-point number giving the electronics gain from which the voltage waveforms originated. The value must be in WCT system of units for [voltage]/[charge] (eg 14.0*wc.mV/wc.fC as expressed in WCT Jsonnet configuration). Note, this is not a unit-less, relative gain.

shaping

a floating-point number giving the electronics shaping time from which the waveforms originated. The value must be expressed in WCT units for [time].

plane

an integer number giving the plane index counting from zero and in the direction of nominal drift. Ie, U=0, V=1, W=2. This value must indicate the plane in which a channel resides in order for the spectra to be applicable.

wirelen

a floating-point number giving a wire length expressed in the WCT system of units for [length]. This value should be representative of (eg, binned over) wires for which the associated spectrum applies.

The GroupNoiseModel provides a model interface for both coherent and incoherent noise where spectra are grouped in some manner. It requires this optional attribute:

group

an integer identifying an abstract group to which channels may be associated. The association to channels may be provided by a WCT channel groups array. The use of groupID as this attribute name is deprecated.

The input spectra can be viewed with:

wirecell-sigproc plot-noise-spectra \
  gen/test/test-noise-spectra.jsonnet orig.pdf

This will consume spectra which are generated by the Jsonnet file which produces a function with the following signature:

function(ngrps=10, nsamples=4096, nsave=64, period=0.5*wc.us,
         fpeak=0.1, rms=1*wc.mV)

It’s arguments are as listed:

ngrps

number of spectral groups to generate. The spectrum from a group will have a fraction grpnum/ngrps of the given rms.

nsamples

number of waveform time samples (number of “ticks”) from which the spectrum is assumed to have originated.

nsave

number of sub-smampled points to produce. This may be chosen equal to nsamples however typical analyses result in far higher frequency resolution than statistical stability (ie, nsamples \(\gg\) nwaves) and thus chosing a small nsave emulates the common case of sub-sampling the result.

period

the waveform sampling period (“tick”) from which the spectrum is assumed to have originated. This must be expressed as a [time] value in the WCT system-of-units.

peak

the location of the spectral peak expressed as a fraction of the Nyquist frequency (0.5/period).

rms

the expected RMS from waveforms generated from the returned mean spectral amplitude. This must be expressed as a [voltage] value in the WCT system-of-units.

See below for guidance on how to provide meaningful values for peak and rms.

The user requires some understanding of the noise spectral model that is used in this test in order to provide proper values. The spectral shape in the frequency domain is chosen to follow the Rayleigh distribution, \[R(x;\sigma) = \frac{x}{\sigma^2}e^{-x^2/(2\sigma^2)},\ x \ge 0\] We will include a constant scaling term so that the full spectral model function is: \[\langle|X_k|\rangle \triangleq S\cdot R_k,\] where we discretize \(R_k \triangleq R(f_k,\sigma_s)\) and define the parameter \(\sigma_s = \mathtt{peak} * F_{Nyquist}\). The \(\sigma_s\) may be chosen to place the peak near that of some real world noise spectrum and the constant scaling term \(S\) may be chosen so that waveforms generated from this mean spectrum will have some (mean) RMS near that of some set of real world noise waveforms.

The choice of the Rayleigh distribution for the spectral shape is motivated by the fact it roughly reproduces the shapes of real-world noise spectra. It is otherwise an ad-hoc choice and not motivated by any physics. In particular, the choice does not relate to the coincidental but important fact that each spectral bin \(k\) is also distributed by a Rayleigh distribution. Its distribution is governed by Rayleigh parameter \(\sigma_k,\ k\in[0,N-1]\) where \(N\) is given by nsamples.

The fact that the spectral bin values are Rayleigh-distributed provides a very practical tool which allows relating the model parameters to the (mean) RMS in time. This is possible because the first two “raw” moments of the Rayleigh distribution are related through the \(\sigma_k\) parameter as:

\[\langle|X_k|\rangle = \sqrt{\frac{\pi}{2}}\sigma_k\] and \[\langle|X_k|^2\rangle = 2\sigma_k^2.\] Solving gives: \[\langle|X_k|\rangle^2 = \frac{\pi}{4} \langle|X_k|^2\rangle,\ k\in[0,N-1].\] We may define RMS on a per-waveform basis in the time domain and relate that to a frequency-domain representation using Perseval/Rayleigh energy theorem: \[\sigma_{rms}^2 = \sum_k|x_k|^2/N = E/N = \sum_k|X_k|^2/N^2.\] And we may form an average \(\langle\cdot\rangle\) over many waveforms, \[\langle \sigma_{rms}^2 \rangle = \sum_k \langle |X_k|^2 \rangle / N^2 = \sum_k \frac{4}{\pi} \langle |X_k| \rangle^2/N^2\] Putting the above all together, we are left to choose \(\sigma_s\) and \(S\) so that the above sum gives desired \(\langle\sigma_{rms}^2\rangle\). We expect to select \(\sigma_s\) so that the model peak will be approximately the same as the peak of some real-world noise spectrum. Taking \(\sigma_s\) as given, we are left to solve for \(S\): \[S^2 = \frac{\pi N^2 \langle\sigma_{rms}^2\rangle}{4 \sum_k R_k^2} \] Thus the rms parameter is identified as providing the desired value of the \(\sqrt{\langle\sigma_{rms}^2\rangle}\). An example with \(N=6000,\ \sigma_{rms}=1\ \mathrm{mV},\ \mathtt{peak}=0.1,\ T=0.5\ \mu\mathrm{s}\) and saving only 100 subsampled points is shown:

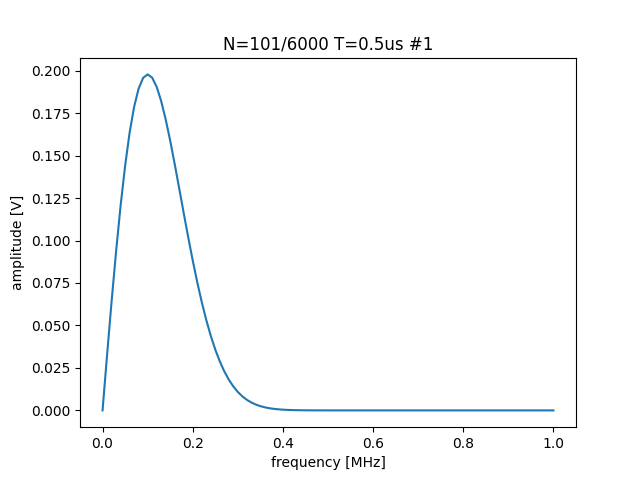
See test-noise-roundtrip.sh for exact command. The commands to reproduce such plots are described next.

The above plot was made with a command like the following:

wirecell-sigproc plot-noise-spectra \
  -A ngrps=1 \
  -A nsamples=6000 \
  -A nsave=100 \
  gen/test/test-noise-spectra.jsonnet \
  specta.pdf

As illustrated, novel values for parameters of the model may be set from the command line. This same Jsonnet file may be used from WCT job configuration. This provides an easy way to define noise where the Rayliegh shape is sufficient to model a desired noise spectrum.

For comparison, an example of a spectrum modeling real-world noise from the ProtoDUNE-SP (PDSP) detector is given:

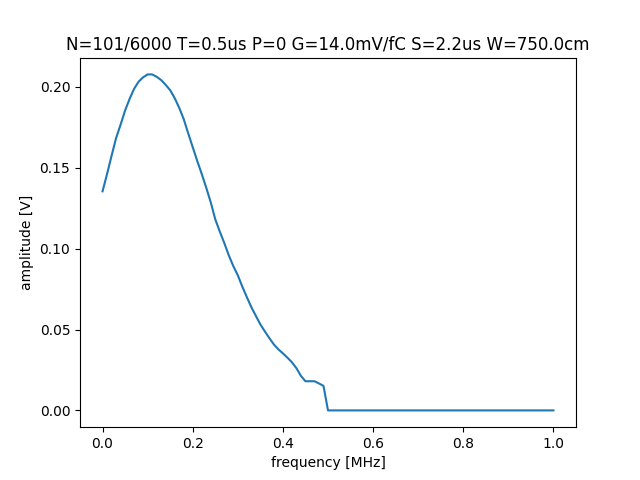
The noise in PDSP is about 4 ADC RMS and its 12 bit ADC sees voltage in the range of 200 to 1600 mV and so expects about 1.3 mV RMS of noise measured in voltage input to the ADC. As a reminder, the simple model above has rms = 1 mV and achieves a smilar peak of 200 mV in amplitude for similar peak and same nsamples.

A main configuration file for wire-cell is provided that uses the same test-noise-spectra.jsonnet described above to provide the input to the round-trip. The round-trip job can be exercised with default parameters like:

$ wire-cell -c  gen/test/test-noise-roundtrip.jsonnet
$ ls -l test-noise-roundtrip-*{npz,json.bz2}

The job flow graph is:

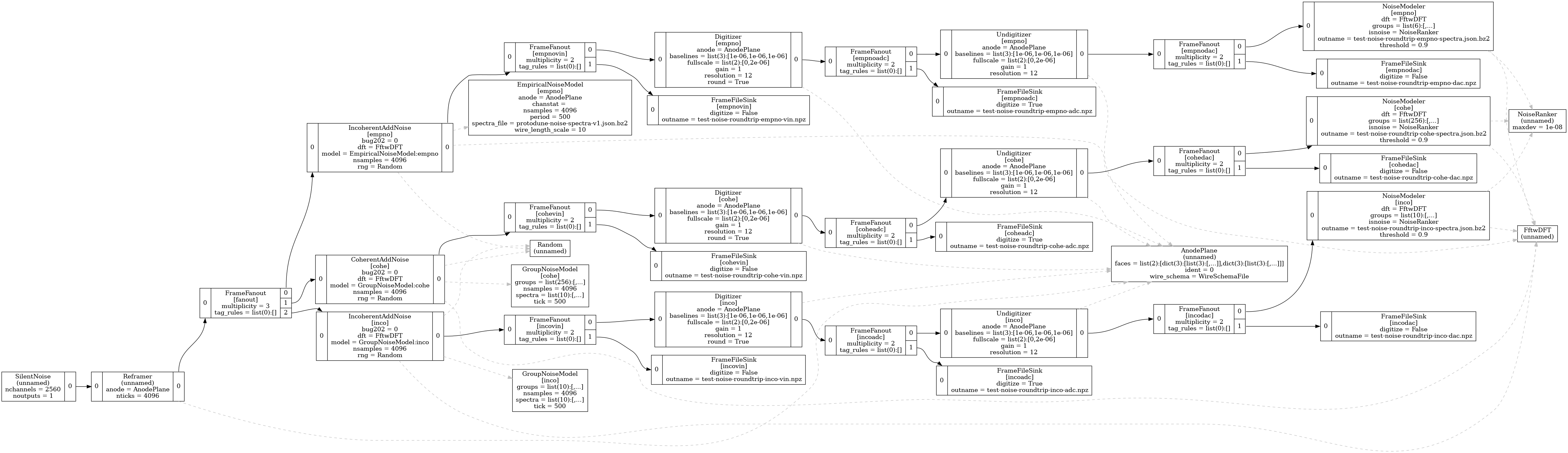
It produces output that represents a cross product of \((inco,cohe) \otimes (adc,dac)\) where

inco

incoherent grouped noise (3 groups)

cohe

coherent grouped noise (10 groups)

adc

the simulated ADC

dac

the ADC rescaled back to voltage level

Each cross produces a .npz file and each noise type results in a .json.bz2 file of output spectra. These too can be visualized

wirecell-sigproc plot-noise-spectra \
  test-noise-roundtrip-inco-spectra.json.bz2 \
  inco-spectra.pdf

wirecell-sigproc plot-noise-spectra \
  test-noise-roundtrip-cohe-spectra.json.bz2 \
  cohe-spectra.pdf

Or, run it all together as:

aux/test/test-noise-roundtrip.sh